When thinking about just about anything that lies on a dimension, it is natural for me to play a little game and imagine what lies at the poles. Personality traits are often thought of as dimensions. It’s advantageous to imagine the manifestations of the ‘most,’ or the ‘least’ of some particular trait, because those images become prototypes, and all that lies between them are transformations.

When I encountered the trait self-complexity, I automatically played my little game. What would someone be like who had infinite self-complexity? It’s impossible, we might say. However, in doing calculus it is. For example, we can examine the equation y = 1\x as x approaches infinity, but we cannot look at the end-point, because it isn’t real. (neither is the point where x approaches 0). If we do the calculus for self-complexity, we find someone(s) who have identities wrapped up in increasingly higher numbers of aspects. Such persons would, by the extrapolations of evidence given in the textbook, be very resistant to stress, at least those caused by perceived social impacts, (Not those stressors that harm the body). Furthermore, such persons would be less prone to mood swings, and particular positive or negative information about them would have less of an impact on their perceived self.

It’s a fun game to play to imagine such a person, or to imagine achieving such a state. I am not sure that many people would trade the mix of happy and sad moods for a more gentle ride. It’s not even possible, is it? It would be a ridiculous enterprise to describe oneself via a humongously intricate personality profile, a task demanding enough to be exhausting on a day-to-day basis. But if we look at the calculus, we see that as the number of personality aspects increases, assuming the there is a finite amount of information to describe, those aspects get more and more specific. And, as the number of aspects approaches infinity, the specificity, or the size of the aspect approaches 0.

There are a number of ways to increase the specificity of our self-descriptions, across dimensions, or within time. If we look at time as our variable (let x be time), then the second last hypothetical individual (lets call him infinite self-complexity minus 1), would be defining themselves moment to moment, and I imagine they would be very frustrated with the whole task. What would the next person do? The last hypothetical person, the one with infinite self-complexity, would just stop defining themselves entirely. Of course this person would appear similar to someone with 0 self-complexity. The head of the process would swing right around and bite itself in the tail. Didn’t someone say, that true knowing, is knowing that you know nothing?

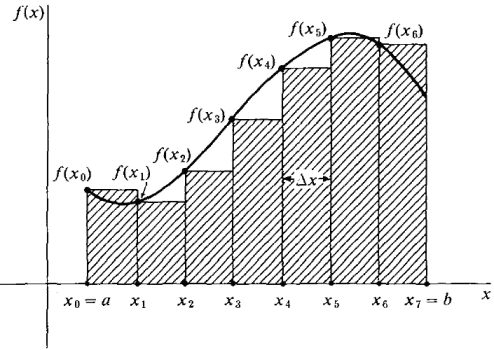
Interestingly there is another form of calculus that allows us to find the area of non-rectangular items. Imagine a curve on an x-y plot. We can find an estimate of the area of that irregular shape by inserting and adding up the area of a number of rectangles. However it’s an estimate because of the overlaps, and the the missing bits. But we can decrease the overlap and the missing bits by increasing the number of rectangles. The true area would be what we would find inserting an infinite number of rectangles. Of course we can’t do that, but we can find the limit to the area as we approach infinity, which gives us a pretty good answer. This might form a good analogy for increasing self-complexity across dimensions. We can see ourselves more accuratly, if we look at increasingly numerous numbers of concepts, but we lose power to grasp that concept as it gets more and more specific, and less observable.

Of course, this little game assumes that the self is finite in the first place, in which case if it isn’t, the whole process is futility ab initio.

what language are you speaking

words, words, words. our language is what has defined our entire state of being. when did we get here? how did we allow this to happen? a number of examples come to mind of how language has limited our experience of the world and ourselves. more importantly ourselves. how could anyone possibly find the articulation to encompass the indescribable? these letters, these symbols, are too small to be used in understanding the meaning of "is".

i came across a video of a young guy talking about embodiment and representation. first of all, it made me long for people that i used to have really mind-numbing conversations with. mind-numbing in the sense that i always found myself getting caught up in the unimaginable, like trying to comprehend the size of the universe. secondly, i found it very comforting to hear that some stranger, somewhere in this world, has had similar questions.

with an impending transition, i've been experiencing a number of emotions. but, when i try to share them with people i cannot quite explain what is going on inside. it gets frustrating because they can't exactly know the balance between excitement and fear, the ratio between joy and anxiety. sometimes i wish i could just touch someone so that they could hear my inner thoughts, and know that silent monologue. but, instead i've had to try to verbalise these things, and without consciously doing it i categorise and label.

in the video, the guy says: all of our thought activity is a function of the way our brains are structured rather than the way the objective world is structured... language is part of our experience, but language is essentially a biological activity. it isn't an objective representation of the world. we can't logically picture reality with human language. like vichenstein said, 'the meaning of a word is the way that it's used in a particular social context. it has no independent meaning in and of itself but within that context'.

this makes me wonder about how we must, every day, somewhat revert to those social transgressions, if i may. that we knowingly restrict ourselves by continuing to encase our experience with the meanings that have been taught to us. i even think it applies to both ends of the spectrum in terms of personal experience. my sister is going through a terrible personal struggle. with the suicidal death of one of her friends she has spun into questioning her own mortality, her ideas about existence, and her understanding of herself as a part of the universe. i know it scares her, but rather than allowing herself to be inside of those feelings she falls back on social constructs of acceptable thoughts and behaviours. apparently she cannot be sad because she has everything that should make her happy. she doesn't think that she's allowed to feel negative because there is someone else who must live with much less than she has. to be fair, sometimes it is good to be reminded that living in canada is a blessing in many ways, and that most of us do have a warm home, an education or opportunities for self-fulfillment, and people that we know and care about. we can easily find ourselves taking those things for granted. but, i don't think it is right that she doesn't give herself the permission to experience the world uniquely.

on the other hand, i also wonder about the l-word. love. so many definitions. but, do we limit our experience of love by using words? in my experience, when you meet someone and grow to love them, you understand that love before your mind thinks it. but, within our society and these constantly changing cultural norms (or abnorms), the labeling of these feelings tends to precede the innate understanding. and sometimes, we claim a love that we never feel at all. why? what do we achieve? do we "fit in"? i would much rather go my entire life in the company of a man who never told me he loved me, but showed me, than hear "i love you" and never truly believe it.

Sodium Anger Supressants

Harvesting an empire go the horses plowing salt beneath the sovereign fields of lore that once produced the finest malt from which ironically the crown exacted tribute to acquire all the horses now employed in pulling horses from the mire

The empire can’t let you become angry, for if you do, you will likely be compelled to act. An active citizenry is detrimental to the pyramidal power structure of the empire. This is why Emperor Obama has recently changed his tone back to one of hope again, hope that by downplaying the new depression we’re all witnessing, things will somehow just get better. Highlighting the bitterness of the new struggle is too real for many Americans. They like the old Obama better, the one at the forefront of some mythical renaissance about to envelop their great land. They like hearing songs about better times beyond George Bush, not speeches about how much money will be required to bail out the large handful of corrupt and teetering Wall Street financial institutions whose vaults were recently revealed to contain nothing more than a few crumpled, yellowed news pages from the Wall Street Journal.
The world’s most powerful banks are falling faster than the speed with which they swindled that cool ten trillion dollars from the lifetime savings of the working and middle classes. This is why we aren’t supposed to be angry, just utterly confused. If we don’t understand the technically incoherent Wall Street lingo, we certainly can’t come to explain how our retirement savings can disappear overnight, or how corporate bankruptcy protections enacted to save a company’s upper echelons can also terminate the majority of the workforce, immediately. If an ordinary citizen could properly do the math and explain in numbers how top corporate executives are able to garner hefty bonuses before stepping into the cockpits of other industries to garnish workers wages, they’d most certainly see before them the highway robbing bankers sanctimoniously wrapping themselves in ambiguous pages of obscure law.
If one hasn’t the vocabulary with which to define oppression, one cannot know that they are a slave. If this is the current state of the union, it is because Americans have been kept fat and satiated at home watching their television sets on pharmaceutical drugs, or otherwise tied up at work sitting through extended, unpaid overtime hours pushing pages through a computer. These corporate bailout shenanigans should have so boldly spurned the people of the United States that it’s a wonder we aren’t seeing pitchforks at the doors of Capitol Hill, especially in the hands of those Americans about to foreclose on homes purchased through predatory lending tactics. Instead, we see Barrack Obama coming to the rescue on TV with his futile government order to stop AIG executives from receiving bonuses they are legally allowed to receive. Everything is okay. You can go back to comfortably watching John Stewart laugh his way through this global financial crisis tonight because, realistically, any anger needed to topple this brutal empire should have been expressed throughout the last eight years of rule. We’re now in the house that complacency built, where the walls are transparent but nobody is looking.

Tragedy In Real Time

Pilot of this airship
I don’t hear a sound
I don’t see a wing tip
All I see is ground
I was on a round trip
First class fare
She was in the front row...I
Couldn’t help but stare...into those eyes
Falling, Falling
Those eyes
So unkind

Pilot of this airship
I don’t hear a sound
I don’t see an airstrip
Turn this ship around
I was on a round trip
First class fare
She was in the front row...I
Saw her sitting there...before too late
Falling, falling
Too late
No rewind

journey through the woods

i followed you into the dark
into a blinding night
a blackness that stole my sight

but you led me home to you
holding my hand so dear
keeping me ever near

you wouldn't let me become afraid
you made me feel more calm
soon we'd be safe and warm

you knew just the right way to go
as if you had learned those steps
you knew what to expect

so i gave myself up to trusting you
and you were my guide
hand-in-hand, by my side

Nemeses

Philistine,
You lost your honor to a boy of thirteen
Out there in the desert
Where the midday sun beats a man unrelentingly

Amen

Levantine,
The games your children play seem very obscene
They kill what they don’t understand
Always enemies

Amen

Always enemies
Always nemeses

Philistine,
You lost your armor but you kept your spleen
Out there in the desert
Where the hallowed sands bury pride so thoroughly

Amen

Levantine,
The ark is missing as it's always been
The truth lay buried in its grave
Painted with the gold of the pharisees

Amen

Always enemies
Always nemeses